Language-Integrated Verification

Types as Theorems, Programs as Proofs

Classic Idea Curry-Howard, Propositions As Types

Types As Theorems

The Refined Type ...

\[\reft{v}{b}{P}\]

... corresponds to the Theorem

\[\mathit{P}\]

Types as Theorems: Example

The Refined Type ...

{-@ type OnePlusOneEqualsTwo = {v:() | 1 + 1 = 2} @-}

... corresponds to the Theorem

\[1 + 1 = 2\]

Programs As Proofs: Example

The Program ...

{-@ easyProof :: OnePlusOneEqualsTwo @-} easyProof = ()

... corresponds to a Proof that

\[1 + 1 = 2\]

Types As Theorems

The Refined Type ...

\[\bindx{n}{\Nat} \rightarrow \reft{v}{b}{P(n)}\]

... corresponds to the Theorem

\[\forall n \in \Nat.\ P(n)\]

Types as Theorems: Example

The Refined Type ...

{-@ type PlusCommutes = n:Int -> m:Int -> { n + m = m + n } @-}

... corresponds to the Theorem

\[\forall n, m.\ n + m = m + n\]

Programs As Proofs: Example

The Program ...

{-@ sillyProof :: PlusCommutes @-} sillyProof n m = ()

... corresponds to a Proof that

\[\forall n, m.\ n + m = m + n\]

Types as Theorems, Programs as Proofs

Code		Math
Types	are	Theorems
Programs	are	Proofs

Those Proofs were Boring

Simple Arithmetic

Automatically proved by SMT Solver

Those Proofs were Boring

Simple Arithmetic

Automatically proved by SMT Solver

How about proofs about user-defined functions?

Beyond automatic SMT, but the user can write proofs

Theorems about Functions

{-@ reflect sum @-} sum :: Int -> Int sum n | n <= 0 = 0 | otherwise = n + sum (n - 1)

How can we prove the the theorems

\(\mathit{sum}(1) = 1\),

\(\mathit{sum}(2) = 3\),

\(\mathit{sum}(3) = 6\).

The annotation

{-@ reflect sum @-}

Automatically gives sum the type

sum :: n:Int -> {v:Int | v = if n == 0 then 0 else n + sum (n-1)}

Reflect Function into Output Type

The type of sum connects implementation and specification

sum :: n:Int -> {v:Int | v = if n == 0 then 0 else n + sum (n-1)}

Reflect Function into Output Type

The type of sum connects implementation and specification

sum :: n:Int -> {v:Int | v = if n == 0 then 0 else n + sum (n-1)}

Key Idea

Calling sum n reveals definition at n to refinement logic!

Reflection at Result Type

{-@ sum3 :: _ -> { sum 3 == 6 } @-} sum3 _ = let s0 = sum 0 -- s0 :: {sum 0 = 0 } s1 = sum 1 -- s1 :: {sum 1 = 1 + sum 0} s2 = sum 2 -- s2 :: {sum 2 = 2 + sum 1} s3 = sum 3 -- s3 :: {sum 3 = 3 + sum 2} in () -- SMT connects the dots.

Key Idea

Calling sum n reveals definition at n to refinement logic!

Structuring Proofs as Calculations

Using combinators from ProofCombinators!

{-@ sum3' :: _ -> { sum 3 = 6 } @-} sum3' _ = sum 3 ==. 3 + sum 2 ==. 3 + 2 + sum 1 ==. 3 + 2 + 1 + sum 0 ==. 6 *** QED

Types as Theorems, Programs as Proofs

Code		Math
Types	are	Theorems
Programs	are	Proofs

Reusing Proofs: Functions as Lemmas

Proofs are functions

Reusing Proofs: Functions as Lemmas

Proofs are functions

Reuse by calling the function

Reusing Proofs: Functions as Lemmas

Proofs are functions

Reuse by calling the function

{-@ sum4 :: _ -> { sum 4 = 10 } @-} sum4 _ = sum 4 ==. 4 + sum 3 ==. 4 + 6 ? sum3 () -- lemma { sum 3 == 6 } ==. 10 *** QED

? is a library operator (read ``because'')

Types as Theorems, Programs as Proofs

Code		Math
Types	are	Theorems
Programs	are	Proofs

Types as Theorems, Programs as Proofs

Code		Math
Types	are	Theorems
Programs	are	Proofs
Functions	are	Lemmas

Proof by Logical Evaluation

Long chains of calculations are tedious

Proof by Logical Evaluation

Long chains of calculations are tedious

Make the machine do the hard work!

A new algorithm to emulate computation in SMT logic

Proof by Logical Evaluation

Long chains of calculations are tedious

Make the machine do the hard work!

A new algorithm to emulate computation in SMT logic

{-@ sum3auto :: _ -> { sum 3 = 6 } @-} sum3auto _ = () {-@ sum4auto :: _ -> { sum 4 = 10 } @-} sum4auto _ = ()

Proof by Induction

Lets prove the theorem

\[\forall n.\ \sum_{i = 0}^n i = \frac{n \times (n + 1)}{2}\]

Proof by Induction

Lets prove the theorem

\[\forall n.\ \sum_{i = 0}^n i = \frac{n \times (n + 1)}{2}\]

that is

\[\forall n \in \Nat.\ 2 \times \mathit{sum}(n) = n \times (n + 1)\]

Proof by Induction

\[\forall n \in \Nat.\ 2 \times \mathit{sum}(n) = n \times (n + 1)\]

{-@ sumPf :: n:Nat -> { 2 * sum n == n * (n + 1) } @-} sumPf :: Int -> () sumPf 0 = 2 * sum 0 ==. 0 *** QED sumPf n = 2 * sum n ==. 2 * (n + sum (n-1)) ==. 2 * (n + ((n - 1) * n)) ? sumPf (n - 1) ==. n * (n + 1) *** QED

Q: What happens if we use the wrong induction?

Types as Theorems, Programs as Proofs

Code		Math
Types	are	Theorems
Programs	are	Proofs
Functions	are	Lemmas

Types as Theorems, Programs as Proofs

Code		Math
Types	are	Theorems
Programs	are	Proofs
Functions	are	Lemmas
Branches	are	Case-Splits

Types as Theorems, Programs as Proofs

Code		Math
Types	are	Theorems
Programs	are	Proofs
Functions	are	Lemmas
Branches	are	Case-Splits
Recursion	is	Induction

Theorems about Data

Recall the list append function:

(++) :: [a] -> [a] -> [a] [] ++ ys = ys (x:xs) ++ ys = x : (xs ++ ys)

Lets prove that the operator is associative

{-@ type AppendAssoc a = xs:[a] -> ys:[a] -> zs:[a] -> { (xs ++ ys) ++ zs = xs ++ (ys ++ zs) } @-}

Theorems about Data: Associativity of `append`

Lets write fill in a calculational proof:

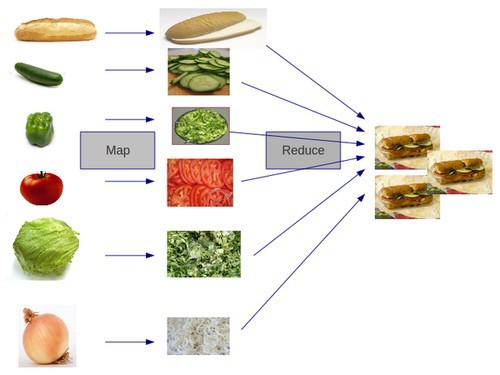
{-@ appendPf :: AppendAssoc a @-} appendPf xs ys zs = () -- Q: Can you help me fill this in?

Case Study: MapReduce

Chunk inputs, Map operation in parallel, and Reduce the results.

Case Study: MapReduce

Chunk inputs, Map operation in parallel, and Reduce the results.

Reduce Theorem

Description

If op is associative then reduce op xs == parallelReduce op xs

Theorem

reduceTheorem
 :: op:(a -> a -> a)                  -- for any op-erator
 -> xs:[a]                            -- for any collection xs
 -> Assoc op                          -- if op is associative
 -> {reduce op xs = parReduce op xs}  -- then parReduce is ok!