Language-Integrated Verification

Binary Search Trees

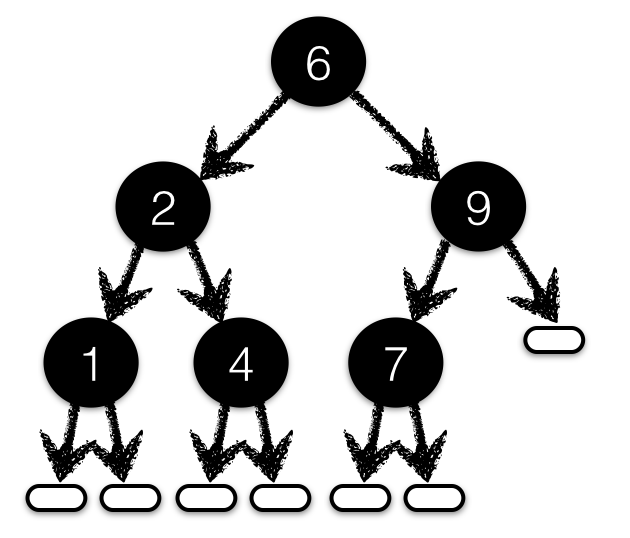
At each node with value key

Left subtree nodes are less than key

Right subtree nodes are greater than key

Binary Search Trees

data BST k v = Leaf | Node { mKey :: k , mVal :: v , mLeft :: BST k v , mRight :: BST k v } ok _ = Node 6 "six" (Node 2 "two" (Node 1 "one" Leaf Leaf) (Node 4 "four" Leaf Leaf) ) (Node 9 "nine" (Node 7 "seven" Leaf Leaf) Leaf )

Legal Binary Search Trees

{-@ data BST k v = Leaf | Node { mKey :: k , mVal :: v , mLeft :: BST k v , mRight :: BST k v } @-} bad _ = Node 6 "six" (Node 2 "two" (Node 1 "one" Leaf Leaf) (Node 4 "four" Leaf Leaf) ) (Node 9 "nine" Leaf (Node 7 "seven" Leaf Leaf) -- NO! key 7 on rhs of 9 )

Exercise: Refine the type to only allow legal BST (e.g. reject bad)

Lookup a Value in a BST

Classic Recursive Traversal

{-@ reflect get @-} get :: (Ord k) => BST k v -> k -> Maybe v get (Node k v l r) key | key == k = Just v | key < k = get l key | otherwise = get r key get Leaf _ = Nothing

Update a Value in a BST

Classic Recursive Traversal

{-@ reflect set @-} set :: (Ord k) => BST k v -> k -> v -> BST k v set (Node k v l r) key val | key == k = Node key val l r | key > k = Node k v (set l key val) r | otherwise = Node k v l (set r key val) set Leaf key val = Node key val Leaf Leaf

Exercise: Oops. Not so classic. What's up?

What Theorems Shall we Prove?

Looks like the type checker automatically verifies legal invariant!

Functional Correctness: McCarthy's Dictionary Laws

set updates the value of the same key

\[\forall m, k, v. \mathrm{get}\ (\mathrm{set}\ m\ k\ v) = v\]

set preserves values of other keys

\[\forall m, k_1, k_2, v. k_1 \not = k_2 \Rightarrow \mathrm{get}\ (\mathrm{set}\ m\ k_2\ v)\ k_1 = \mathrm{get}\ m\ k_1\]

Specifying the Laws as Types

set updates the value of the same key

m:_ -> k:_ -> v:_ -> {get (set m k v) k = Just val}

set preserves values of other keys

m:_ -> k1:_ -> k2:{k2 /= k1} -> v:_ -> {get (set m k2 v) k1 = get m k1}

Verifying the Laws as Types

{-@ lem_get_eq :: m:_ -> key:_ -> val:_ -> { get (set m key val) key = Just val } @-} lem_get_eq m key val = undefined

Exercise: Shall we try to fill the proof in?

Verifying the Laws as Types

Proof of the second law is similar

Split cases and recursion (aka induction)...

{-@ lem_get_neq :: m:_ -> k1:_ -> k2:{k2 /= k1} -> v:_ -> { get (set m k2 v) k1 = get m k1 } @-} lem_get_neq Leaf k1 k2 _ | k1 < k2 = () | otherwise = () lem_get_neq (Node k v l r) k1 k2 v2 | k1 < k, k < k2 = () | k == k2 = () | k1 == k, k < k2 = () | k2 < k, k == k1 = () | k2 < k, k < k1 = () | k1 < k, k2 < k = lem_get_neq l k1 k2 v2 | k < k1, k < k2 = lem_get_neq r k1 k2 v2

Introduction

Part I: Refinements 101

Case Study: Vector Bounds

Part II: Properties of Structures

Case Study: Sorting, Interpreter